If you have decided based on your setup and requirements, that it is best to perform the calibration using the AQS12 target, you fill find a detailed guide in the following sections.
With the AQS12 calibration the following calibration corrections can be estimated:
| Calibration Correction | Link to Calibration Theory |
|---|---|
| Homography | Transformation of Range Map Coordinates to Metric Coordinates |
| Encoder step (scale in Y) | |
| Correction of inclined laser plane | Correction of an Inclined Laser Plane and Extrinsic Calibration |
| Rotation and translation to given coordinate system (rigid-body transformation) |
In order to estimate the calibration corrections, a target with precisely defined reference points is required. CVB currently supports a diamond-shaped calibration pattern, called AQS12 for this purpose. The AQS12 has a distinct shape with 8 planes and 12 feature points resulting from the intersection points of these planes. While the overall size of the target can vary, the proportions of the example AQS12 shown in this section should be largely maintained, as they are important for the internal algorithm. Additionally, the correct order of the points on the pattern must be observed, depending on the camera setup.
The dimensions of the calibration target should be similar to the example shown in the figures below. In any case it should meet the following requirements:
The following figures show an example AQS12 with optimal dimensions. It is best to scale it to the dimensions of your current setup.
|
|
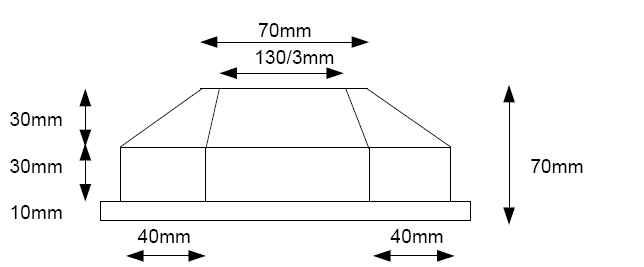
AQS12 Side View |
The world coordinates of the reference points for the example shown in the figure above are listed in the following table:
| Point | X [mm] | Y [mm] | Z [mm] | |
|---|---|---|---|---|
| movement direction away from camera | movement direction towards camera | |||
| 1 | 0 | 35 | -35 | 60 |
| 2 | 10 | 21.667 | -21.667 | 60 |
| 3 | 10 | -21.667 | 21.667 | 60 |
| 4 | 0 | -35 | 35 | 60 |
| 5 | -10 | -21.667 | 21.667 | 60 |
| 6 | -10 | 21.667 | -21.667 | 60 |
| 7 | 0 | 75 | -75 | 30 |
| 8 | 30 | 35 | -35 | 30 |
| 9 | 30 | -35 | 35 | 30 |
| 10 | 0 | -75 | 75 | 30 |
| 11 | -30 | -35 | 35 | 30 |
| 12 | -30 | 35 | -35 | 30 |
| Height | 60 | |||
The first column represents the x-coordinate, the second the y-coordinate, and the third the z-coordinate. The single value in the last line specifies the height difference between the roof and the base plane. Pay close attention to the order of the points: If the movement direction is towards the camera, the point order will change, as explained in the next section.
It is worth noting that the vertical walls of the calibration target are not mandatory. The target can also consist of just the base and top planes with six faces (see the figure below):
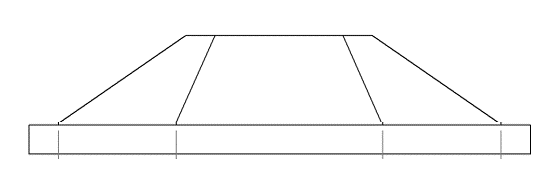
Additionally to the appropriate design of the target, the following specifications should be considered during the acquisition:
Note, that the order of the reference points in the range map depends on the direction of movement and the camera's mounting. If the movement direction is away from the camera, the point order in the range map corresponds directly to the real-world arrangement. In this case the 7th point will appear at the top, and the 10th point at the bottom:
If the movement direction is towards the camera, the points are mirrored along the y-axis (or along the rows). In this case, the 10th point will appear in the range map at the top, and the 7th point at the bottom:
AQS12Piece class (e.g., Cvb::Foundation::Metric::AQS12::AQS12Piece, Stemmer.Cvb.Foundation.AQS12Piece or cvb.foundation.AQS12Piece), it is essential to understand that the point order is determined by the range map's coordinate system. In the range map, the topmost point corresponds to point #7, and the bottommost point corresponds to point #10.If the point order appears mirrored in the range map due to the camera's orientation or mounting, you must adjust the corresponding real-world points passed to the AQS12Piece object to match this mirrored order. The following table illustrates how the point numbers in the range map relate to their counterparts in the real-world coordinate system, assuming that the movement direction is towards the camera:
| roof | base | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Point number as used in the AQS12Piece class. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Corresponding point number on the real-world AQS12 target. | 4' | 3' | 2' | 1' | 6' | 5' | 10' | 9' | 8' | 7' | 12' | 11' |
By defining the points as shown above, the calibrated and transformed points will be in a right-handed trihedron. A code example demonstrating how to define the reference points using the AQS12Piece class is available here.
Recommendation for rectified point clouds:
For subsequent image processing on a rectified point cloud, it is often advisable to transform the point cloud into a left-handed trihedron, as image coordinates typically follow a left-handed system.
When rectifying a point cloud, the x-coordinates correspond to the image columns, and the y-coordinates correspond to the image rows. While the X-axis of the point cloud and the column axis of the image both point to the right, the Y-axis of a right-handed trihedron points upward, whereas the row axis of the image points downward. Conversely, the Y-axis of a left-handed trihedron also points downward, aligning with the image coordinate system. As a result, rectifying a point cloud from a right-handed trihedron will cause it to appear mirrored in the image.
To transform the point cloud into a left-handed trihedron, mirror the input reference points by multiplying their y-coordinates by -1.
It is essential to distinguish between two operations:
When working with idealized coordinates, such as those derived from a CAD model (like for the example AQS12 depicted above), these operations may yield identical results. However, with precisely measured reference coordinates, the two approaches can produce different outcomes. The table below demonstrates this distinction with exemplary coordinates for points #1 and #4:
| Original Coordinates | Point Order Mirrored/Points Swapped | Y Coordinates Mirrored | |
|---|---|---|---|
| #1 | (0,30,60.1) | (0,-30,59.9) | (0,-30,60.1) |
| #4 | (0,-30,59.9) | (0,30,60.1) | (0,30,59.9) |
The following sections will provide a detailed guide on how to perform the AQS12 calibration using the CVB SDK. Using the AQS12 you can perform three types of calibration:
| Calibration Correction | Extrinsic Calibration | Intrinsic and Extrinsic Calibration | |
|---|---|---|---|
| Use Case 1 | Use Case 2 | Use Case 3 | |
| Homography | ✓ | ||
| Encoder step (scale in Y) | ✓ | ✓ | |
| Correction of inclined laser plane | ✓ | ✓ | |
| Rotation and translation to given coordinate system (rigid-body transformation) | ✓ | ✓ | ✓ |
Example programs for each use case are available in C++, .NET and Python. These can be found in your CVB setup under the following directories:
Alternatively, the examples can be accessed via the following links:
| Extrinsic Calibration | Intrinsic and Extrinsic Calibration | ||
|---|---|---|---|
| Use Case 1 | Use Case 2 | Use Case 3 | |
| C++ | CppMetricCalibrationInclinationLaserPlane | CppMetricCalibrationRigidBodyTrafo | CppMetricCalibration |
| .NET | Metric3DCalibrationLaserPlane | Metric3DCalibrationRigidBodyTransform | Metric3DCalibration |
| Python | MetricCalibrationInclinationLaserPlane | MetricCalibrationRigidBodyTransformation | MetricCalibration |
The estimation of an intrinsic and/or extrinsic calibration using the AQS12 target is implemented in the CVMetric.dll. To execute the code snippets provided in this documentation, following DLLs are additionally required:
To utilize this functionality, the following namespaces and include files are required:
Once a stable AQS12 target with precisely measured coordinates is manufactured and a range map of the target is acquired, the calibration process can begin. The first step involves defining the reference points using the AQS12Piece class. For critical details about the camera setup and the correct point order, refer to this section.
In addition to specifying the reference points, you can provide the target's height, i.e. the height difference between roof and base plane. However, this value is optional if the reference z-coordinate of the base plane is set to zero. In such cases, you can leave the height parameter as zero, allowing the algorithm to calculate the target’s height automatically.
The AQS12Piece object is required as an initial step for creating a calibration configuration object. For more details, refer to the documentation of Cvb::Foundation::Metric::CalibrationConfiguration, Stemmer.Cvb.Foundation.CalibrationConfiguration and cvb.foundation.CalibrationConfiguration or to the following sections.
If you only need to perform an extrinsic calibration, you will require a calibrated point cloud. This means your sensor must either provide a point cloud directly or a range map paired with a calibration file. If you have already performed an intrinsic calibration of your setup using the ZigZag target, you can proceed with extrinsic calibration as a subsequent step, too.
To get started, follow these initial steps:
The section Correction of an Inclined Laser Plane and Extrinsic Calibration explains how an inclined laser plane affects the shear and scale of x, y, and z coordinates. Overall, the transformation of intrinsically calibrated point clouds to world coordinates involves shear, scale, rotation, and translation, as illustrated below:
The shear, scale, and rotation matrices can be combined into a general affine transformation matrix.
In CVB, there are two approaches to estimate the transformation:
AffineMatrix. This method solves a linear system of equations, making it computationally straightforward.SpecificTransformationParameters. While this approach solves a non-linear system of equations—which might occasionally fail to converge to a reasonable result—it provides more accurate error estimates and thus is generally recommended.By default, CVB uses the SpecificTransformationParameters model for extrinsic calibration, with encoder step estimation enabled.
To perform the calibration, create an extrinsic calibration configuration object using the previously created AQS12Piece first:
With the previously created calibration configuration object, the segementor object and the point cloud, you can perform the estimation of the calibration parameters:
The calibration function provides the following results:
SpecificTransformationParameters is selected as extrinsic calibration model, the calibration also provides parameters for shear, scale, and rotation.Once the calibration results are obtained, it is essential to verify their plausibility and accuracy. For detailed guidance, refer to the section Validation of Calibration.
If you already have a calibrated point cloud with metric x, y and z coordinates free of errors caused by an inclined laser plane, but wish to transform it into a global coordinate system (e.g., when using multiple sensors), a rigid-body transformation can be applied.
Using the AQS12Piece object, and the segementor object created earlier, you can estimate the rigid-body transformation as follows:
The function for estimating the rigid-body transformation produces the following results:
Once the calibration results are obtained, it is essential to verify their plausibility and accuracy. For detailed guidance, refer to the section Validation of Calibration.
If you require both extrinsic and intrinsic calibration, the homography can additionally be estimated using the AQS12 target. However, this method is relatively imprecise and is only suitable for low-accuracy applications. For high-precision measurements, where accurate intrinsic calibration is needed to correct lens distortion and laser line deformation, the ZigZag calibration provided by Stemmer Imaging is recommended.
Begin by loading a range map containing the AQS12 target, then create a segmentor for range maps and a calibration configuration object:
By default, the calculation of the homography and the estimation of the encoder step is enabled, with SpecificTransformationParameters set as extrinsic calibration model. For more details about the extrinsic calibration model, refer to Use Case 1: Correcting an Inclined Laser Plane.
Next, proceed with the calibration estimation:
The calibration function generates a new calibrator object, which contains the following results:
SpecificTransformationParameters is selected as the extrinsic calibration model, the calibration also provides parameters for shear, scale, and rotation.Once the calibration results are obtained, it is essential to verify their plausibility and accuracy. For detailed guidance, refer to the section Validation of Calibration.
Calibration results may sometimes not meet the desired accuracy or expectations. This section provides guidance on identifying potential issues and improving calibration outcomes.
If the calibration completes without errors, the first step is to evaluate the residuals. Residuals smaller than the desired accuracy generally indicate a successful calibration. However, it’s important to note that residuals reflect the accuracy only within the area of the AQS12 target. Measurements taken far from the target area may have higher errors, as residual errors propagate with an increasing distance to the calibration target. Therefore, it is crucial to ensure that the calibration target adequately covers the area where measurements will be performed in the future.
To verify the accuracy further, it is recommended to acquire additional data using a target with known dimensions. The AQS12 target itself can also serve this purpose, providing a reliable reference for validating the calibration's accuracy.
If the calibration results appear implausible, consider the following checks:
1. Were the AQS12 points extracted correctly?
Refer to section AQS12 Segmentation and Point Extraction for detailed guidance on segmenting the faces of the AQS12 target and extracting the intersection points.
2. Are the reference points of the AQS12 target precisely measured?
For high-precision applications, it is essential to use a target made from a stable material. Additionally, the target's reference points must be measured with a precision exceeding the desired accuracy for the calibration.
3. Is the order of the reference points correct?
Verify that the reference points are ordered correctly. This step is particularly critical for precisely measured targets, as swapped or mirrored points can lead to errors. Detailed advice on maintaining the correct point order can be found here.
In most cases, implausible results stem from incorrect segmentation of the AQS12 target faces. Then the AQS12 points cannot be determined correctly.
During segmentation, the range map pixels (or pixels of the rectified point cloud) are clustered using the k-means algorithm. Each cluster corresponds to an AQS12 face, and a plane is subsequently fitted to each face. The intersection points between three neighboring planes are then calculated.
The code snippet below demonstrates how to generate an image of the segmented AQS12 faces and obtain a list of the extracted AQS12 points. Note that these points are projected onto the base plane, as they are derived from the intersection of the segmented faces.