Double precision 3x3 matrix struct. More...

Inherits IEquatable< Matrix3D >.

Public Member Functions
	Matrix3D (double[] row1, double[] row2, double[] row3)
	Constructor. More...

	Matrix3D (double[,] arr)
	Constructor. More...

	Matrix3D (double a11, double a12, double a13, double a21, double a22, double a23, double a31, double a32, double a33)
	Constructor. More...

	Matrix3D (RotationAngles3D rotationAngles)
	Constructor. More...

	Matrix3D (RotationAngles3D rotationAngles, Factors3D scale)
	Constructor. More...

RotationAngles3D	RotationAngles ()
	Computes the Euler angles from the matrix. More...

Tuple< RotationAngles3D, Factors3D, double >	RotationAnglesScale ()
	Computes the Euler angles and scaling from the matrix. More...

void	Invert ()
	Inverts this matrix in-place if possible. More...

Matrix3D	Inverse ()
	Get the inverse of this matrix if possible. More...

override bool	Equals (object obj)
	Indicates whether this instance and the given obj are equal. More...

bool	Equals (Matrix3D obj)
	Indicates whether this instance and the given obj are equal. More...

override int	GetHashCode ()
	Returns the hash code for this instance. More...

override string	ToString ()
	String conversion. More...

Static Public Member Functions
static Matrix3D	operator+ (Matrix3D lhs, Matrix3D rhs)
	Addition operator. More...

static Matrix3D	operator- (Matrix3D lhs, Matrix3D rhs)
	Subtraction operator. More...

static Matrix3D	operator* (Matrix3D lhs, Matrix3D rhs)
	Multiplication operator. More...

static bool	operator== (Matrix3D lhs, Matrix3D rhs)
	Equality comparison operator. More...

static bool	operator!= (Matrix3D lhs, Matrix3D rhs)
	Unequality comparison operator. More...

Static Public Attributes
static readonly Matrix3D	Identity
	The identity element.

Properties
double	A11 `[get, set]`
	Top left matrix element.

double	A12 `[get, set]`
	Top middle matrix element.

double	A13 `[get, set]`
	Top right matrix element.

double	A21 `[get, set]`
	Mid left matrix element.

double	A22 `[get, set]`
	Mid matrix element.

double	A23 `[get, set]`
	Mid right matrix element.

double	A31 `[get, set]`
	Bottom left matrix element.

double	A32 `[get, set]`
	Bottom mid matrix element.

double	A33 `[get, set]`
	Bottom right matrix element.

double	this[int row, int column] `[get, set]`
	Index access. More...

Detailed Description

Double precision 3x3 matrix struct.

Constructor & Destructor Documentation

◆ Matrix3D() [1/5]

Matrix3D	(	double[]	row1,
		double[]	row2,
		double[]	row3
	)

Constructor.

Parameters

row1	First component row.
row2	Second component row.
row3	Third component row.

Exceptions

IndexOutOfRangeException	When one of the given rows has less than three values.
NullReferenceException	When one of the given rows is null.

◆ Matrix3D() [2/5]

Matrix3D ( double arr[,] )

Constructor.

Parameters

arr	A 3x3 array containing the matrix values.

Exceptions

IndexOutOfRangeException	When the given arr is smaller than 3x3.
NullReferenceException	If the given arr is null.

◆ Matrix3D() [3/5]

Matrix3D	(	double	a11,
		double	a12,
		double	a13,
		double	a21,
		double	a22,
		double	a23,
		double	a31,
		double	a32,
		double	a33
	)

Constructor.

Parameters

a11	Top left matrix element.
a12	Top middle matrix element.
a13	Top right matrix element.
a21	Mid left matrix element.
a22	Mid matrix element.
a23	Mid right matrix element.
a31	Bottom left matrix element.
a32	Bottom mid matrix element.
a33	Bottom right matrix element.

◆ Matrix3D() [4/5]

Matrix3D ( RotationAngles3D rotationAngles )

Constructor.

Creates a rotation matrix from the given Euler angles.

The rotation matrix R is computed via:

where
alpha, beta, gamma are the rotation angles around x, y, z.

Parameters

rotationAngles Rotation angles to create matrix from.

Exceptions

CvbException When creating the matrix failed.

◆ Matrix3D() [5/5]

Matrix3D	(	RotationAngles3D	rotationAngles,
		Factors3D	scale
	)

Constructor.

Creates a rotation matrix from the given Euler angles and scaling.

Note, that the scaling is applied before rotation:

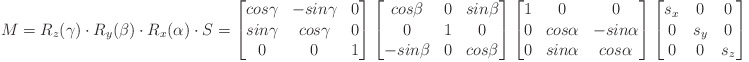
where
alpha, beta, gamma are the rotation angles around x, y, z.
s_x, s_y, s_z are the scaling factors for x, y, z.

Parameters

rotationAngles	Rotation angles.
scale	Scaling factors.

Exceptions

CvbException When creating the matrix failed.

Member Function Documentation

◆ Equals() [1/2]

bool Equals ( Matrix3D obj )

Indicates whether this instance and the given obj are equal.

Parameters

obj	Object to compare to.

Returns: True if obj and this instance represent the same value; otherwise, false.

◆ Equals() [2/2]

override bool Equals ( object obj )

Indicates whether this instance and the given obj are equal.

Parameters

obj	Object to compare to.

Returns: True if obj and this instance are the same type and represent the same value; otherwise, false.

◆ GetHashCode()

override int GetHashCode ( )

Returns the hash code for this instance.

Returns: A 32-bit signed integer that is the hash code for this instance.

◆ Inverse()

Matrix3D Inverse ( )

Get the inverse of this matrix if possible.

Returns: Inverse.

Exceptions

DivideByZeroException If the matrix cannot be inverted.

◆ Invert()

void Invert ( )

Inverts this matrix in-place if possible.

Exceptions

DivideByZeroException If the matrix cannot be inverted.

◆ operator!=()

static bool operator!=	(	Matrix3D	lhs,
		Matrix3D	rhs
	)

static

Unequality comparison operator.

Parameters

lhs	Left hand side operand.
rhs	Right hand side operand.

Returns: True if lhs != rhs , otherwise false.

◆ operator*()

static Matrix3D operator*	(	Matrix3D	lhs,
		Matrix3D	rhs
	)

static

Multiplication operator.

Parameters

lhs	Left hand side operand.
rhs	Right hand side operand.

Returns: Product of lhs and rhs .

◆ operator+()

static Matrix3D operator+	(	Matrix3D	lhs,
		Matrix3D	rhs
	)

static

Addition operator.

Parameters

lhs	Left hand side operand.
rhs	Right hand side operand.

Returns: Sum of lhs and rhs .

◆ operator-()

static Matrix3D operator-	(	Matrix3D	lhs,
		Matrix3D	rhs
	)

static

Subtraction operator.

Parameters

lhs	Left hand side operand.
rhs	Right hand side operand.

Returns: Difference of lhs and rhs .

◆ operator==()

static bool operator==	(	Matrix3D	lhs,
		Matrix3D	rhs
	)

static

Equality comparison operator.

Parameters

lhs	Left hand side operand.
rhs	Right hand side operand.

Returns: True if lhs == rhs , otherwise false.

◆ RotationAngles()

RotationAngles3D RotationAngles ( )

Computes the Euler angles from the matrix.

The matrix is interpreted as a rotation matrix R:

where
alpha, beta, gamma are the rotation angles around x, y, z.

Note: If the resulting beta (angle around y) is outside the range ]-90° .. 90°[ , the computation of the Euler angles is ambiguous (rotation direction may be inversed).

Returns: Rotation angles around x, y and z.

Exceptions

CvbException When matrix is not a valid rotation matrix.

◆ RotationAnglesScale()

Tuple< RotationAngles3D, Factors3D, double > RotationAnglesScale ( )

Computes the Euler angles and scaling from the matrix.

The transformation matrix M is interpreted as:

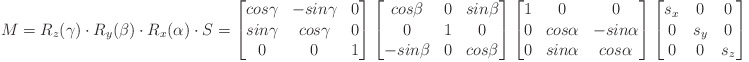
where
alpha, beta, gamma are the rotation angles around x, y, z.
s_x, s_y, s_z are the scaling factors for x, y, z.

If the matrix only contains rotation and scaling, i.e. it is not noisy, then the scaling factors are computed from the normed matrix and threfore positive as a start. If the determinant of the normed matrix is -1, the scaling factor in z is set to a negative value.

If calculating the rotation and scaling from the matrix without approximation is successful the precision value is set to -1. Otherwise an approximation is calculated. This is the case for non-valid rotation matrices (e.g. due to noise). Then the rotation angles and scaling factors are estimated using the Nelder-Mead algorithm. Therefore a cost function is set up and minimized over several iterations. The minimum value after the iteration stopped is stored to precision. If the given matrix is valid and not noisy, the precision will be very low. Note, that this estimation does not work for large scaling factors or if all scaling factors are negative. In this case the output precision will be large (in general greater 1). Then please norm your matrix first by dividing all matrix elements by a matrix norm (e.g. the Frobenius norm or other).

Note: If one of the resulting angles is outside the range ]-90° .. 90°[ or one of the scaling factors is negative, the computation of the Euler angles and the scaling factors is ambiguous (rotation direction may be inversed, negative scaling is the same as rotation about 180 degree).

Returns: Tuple containing Rotation angles, scaling and precision of approximation.

Exceptions

CvbException When calculating the rotation angles and scale failed.

◆ ToString()

override string ToString ( )

String conversion.

Returns: string representation of this MatrixD

Property Documentation

◆ this[int row, int column]

double this[int row, int column]

getset

Index access.

Parameters

row	The row, or "Y" index to get.
column	The column, or "X" index to get.

Returns: Value at the specified position.

Public Member Functions

Static Public Member Functions

Static Public Attributes

Properties

Detailed Description

Constructor & Destructor Documentation

◆ Matrix3D() [1/5]

◆ Matrix3D() [2/5]

◆ Matrix3D() [3/5]

◆ Matrix3D() [4/5]

◆ Matrix3D() [5/5]

Member Function Documentation

◆ Equals() [1/2]

◆ Equals() [2/2]

◆ GetHashCode()

◆ Inverse()

◆ Invert()

◆ operator!=()

◆ operator*()

◆ operator+()

◆ operator-()

◆ operator==()

◆ RotationAngles()

◆ RotationAnglesScale()

◆ ToString()

Property Documentation

◆ this[int row, int column]