Double precision 3x3 matrix struct. More...
Inherits IEquatable< Matrix3D >.
Public Member Functions | |
| Matrix3D (double[] row1, double[] row2, double[] row3) | |
| Constructor. More... | |
| Matrix3D (double[,] arr) | |
| Constructor. More... | |
| Matrix3D (double a11, double a12, double a13, double a21, double a22, double a23, double a31, double a32, double a33) | |
| Constructor. More... | |
| Matrix3D (RotationAngles3D rotationAngles) | |
| Constructor. More... | |
| Matrix3D (RotationAngles3D rotationAngles, Factors3D scale) | |
| Constructor. More... | |
| RotationAngles3D | RotationAngles () |
| Computes the Euler angles from the matrix. More... | |
| Tuple< RotationAngles3D, Factors3D, double > | RotationAnglesScale () |
| Computes the Euler angles and scaling from the matrix. More... | |
| void | Invert () |
| Inverts this matrix in-place if possible. More... | |
| Matrix3D | Inverse () |
| Get the inverse of this matrix if possible. More... | |
| override bool | Equals (object obj) |
| Indicates whether this instance and the given obj are equal. More... | |
| bool | Equals (Matrix3D obj) |
| Indicates whether this instance and the given obj are equal. More... | |
| override int | GetHashCode () |
| Returns the hash code for this instance. More... | |
| override string | ToString () |
| String conversion. More... | |
Static Public Member Functions | |
| static Matrix3D | operator+ (Matrix3D lhs, Matrix3D rhs) |
| Addition operator. More... | |
| static Matrix3D | operator- (Matrix3D lhs, Matrix3D rhs) |
| Subtraction operator. More... | |
| static Matrix3D | operator* (Matrix3D lhs, Matrix3D rhs) |
| Multiplication operator. More... | |
| static bool | operator== (Matrix3D lhs, Matrix3D rhs) |
| Equality comparison operator. More... | |
| static bool | operator!= (Matrix3D lhs, Matrix3D rhs) |
| Unequality comparison operator. More... | |
Static Public Attributes | |
| static readonly Matrix3D | Identity |
| The identity element. | |
Properties | |
| double | A11 [get, set] |
| Top left matrix element. | |
| double | A12 [get, set] |
| Top middle matrix element. | |
| double | A13 [get, set] |
| Top right matrix element. | |
| double | A21 [get, set] |
| Mid left matrix element. | |
| double | A22 [get, set] |
| Mid matrix element. | |
| double | A23 [get, set] |
| Mid right matrix element. | |
| double | A31 [get, set] |
| Bottom left matrix element. | |
| double | A32 [get, set] |
| Bottom mid matrix element. | |
| double | A33 [get, set] |
| Bottom right matrix element. | |
| double | this[int row, int column] [get, set] |
| Index access. More... | |
Double precision 3x3 matrix struct.
| Matrix3D | ( | double[] | row1, |
| double[] | row2, | ||
| double[] | row3 | ||
| ) |
Constructor.
| row1 | First component row. |
| row2 | Second component row. |
| row3 | Third component row. |
| IndexOutOfRangeException | When one of the given rows has less than three values. |
| NullReferenceException | When one of the given rows is null. |
| Matrix3D | ( | double | arr[,] | ) |
Constructor.
| arr | A 3x3 array containing the matrix values. |
| IndexOutOfRangeException | When the given arr is smaller than 3x3. |
| NullReferenceException | If the given arr is null. |
| Matrix3D | ( | double | a11, |
| double | a12, | ||
| double | a13, | ||
| double | a21, | ||
| double | a22, | ||
| double | a23, | ||
| double | a31, | ||
| double | a32, | ||
| double | a33 | ||
| ) |
Constructor.
| a11 | Top left matrix element. |
| a12 | Top middle matrix element. |
| a13 | Top right matrix element. |
| a21 | Mid left matrix element. |
| a22 | Mid matrix element. |
| a23 | Mid right matrix element. |
| a31 | Bottom left matrix element. |
| a32 | Bottom mid matrix element. |
| a33 | Bottom right matrix element. |
| Matrix3D | ( | RotationAngles3D | rotationAngles | ) |
Constructor.
Creates a rotation matrix from the given Euler angles.
The rotation matrix R is computed via:
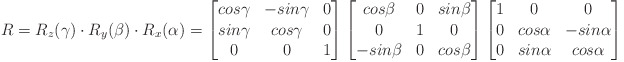
where
alpha, beta, gamma are the rotation angles around x, y, z.
| rotationAngles | Rotation angles to create matrix from. |
| CvbException | When creating the matrix failed. |
| Matrix3D | ( | RotationAngles3D | rotationAngles, |
| Factors3D | scale | ||
| ) |
Constructor.
Creates a rotation matrix from the given Euler angles and scaling.
Note, that the scaling is applied before rotation:
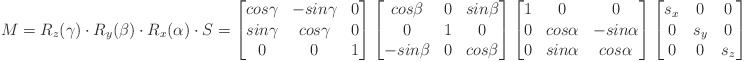
where
alpha, beta, gamma are the rotation angles around x, y, z.
sx, sy, sz are the scaling factors for x, y, z.
| rotationAngles | Rotation angles. |
| scale | Scaling factors. |
| CvbException | When creating the matrix failed. |
| bool Equals | ( | Matrix3D | obj | ) |
Indicates whether this instance and the given obj are equal.
| obj | Object to compare to. |
| override bool Equals | ( | object | obj | ) |
Indicates whether this instance and the given obj are equal.
| obj | Object to compare to. |
| override int GetHashCode | ( | ) |
Returns the hash code for this instance.
| Matrix3D Inverse | ( | ) |
Get the inverse of this matrix if possible.
| DivideByZeroException | If the matrix cannot be inverted. |
| void Invert | ( | ) |
Inverts this matrix in-place if possible.
| DivideByZeroException | If the matrix cannot be inverted. |
Unequality comparison operator.
| lhs | Left hand side operand. |
| rhs | Right hand side operand. |
Multiplication operator.
| lhs | Left hand side operand. |
| rhs | Right hand side operand. |
Addition operator.
| lhs | Left hand side operand. |
| rhs | Right hand side operand. |
Subtraction operator.
| lhs | Left hand side operand. |
| rhs | Right hand side operand. |
Equality comparison operator.
| lhs | Left hand side operand. |
| rhs | Right hand side operand. |
| RotationAngles3D RotationAngles | ( | ) |
Computes the Euler angles from the matrix.
The matrix is interpreted as a rotation matrix R:
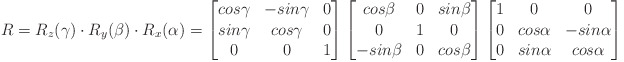
where
alpha, beta, gamma are the rotation angles around x, y, z.
| CvbException | When matrix is not a valid rotation matrix. |
| Tuple< RotationAngles3D, Factors3D, double > RotationAnglesScale | ( | ) |
Computes the Euler angles and scaling from the matrix.
The transformation matrix M is interpreted as:
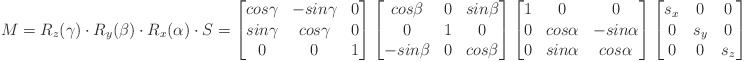
where
alpha, beta, gamma are the rotation angles around x, y, z.
sx, sy, sz are the scaling factors for x, y, z.
If the matrix only contains rotation and scaling, i.e. it is not noisy, then the scaling factors are computed from the normed matrix and threfore positive as a start. If the determinant of the normed matrix is -1, the scaling factor in z is set to a negative value.
If calculating the rotation and scaling from the matrix without approximation is successful the precision value is set to -1. Otherwise an approximation is calculated. This is the case for non-valid rotation matrices (e.g. due to noise). Then the rotation angles and scaling factors are estimated using the Nelder-Mead algorithm. Therefore a cost function is set up and minimized over several iterations. The minimum value after the iteration stopped is stored to precision. If the given matrix is valid and not noisy, the precision will be very low. Note, that this estimation does not work for large scaling factors or if all scaling factors are negative. In this case the output precision will be large (in general greater 1). Then please norm your matrix first by dividing all matrix elements by a matrix norm (e.g. the Frobenius norm or other).
| CvbException | When calculating the rotation angles and scale failed. |
| override string ToString | ( | ) |
String conversion.
|
getset |
Index access.
| row | The row, or "Y" index to get. |
| column | The column, or "X" index to get. |