Functions to create new PointCloud objects by transforming their points. More...
Data Structures | |
| struct | CVC3DTransformation |
| Affine transformation matrix. More... | |
Typedefs | |
| typedef double | CVC3DMatrix[3][3] |
| Row-major 3x3 matrix. More... | |
| typedef double | CVC3DMatrixH[4][4] |
| Row-major 4x4 matrix. More... | |
| typedef double | CVC3DVector[3] |
| x, y, z vector. More... | |
Functions | |
| cvbres_t | CVC3DAlignToXYPlane (const CVC3DPlane &Plane, CVC3DTransformation &Transformation) |
| Calculates a rigid body transformation that maps a specified plane into the xy plane of the global coordinate system. More... | |
| cvbres_t | CVC3DCreateConvertedPointCloud (CVCOMPOSITE PointCloudIn, cvbval_t Flags, CVCOMPOSITE &PointCloudOut) |
| Creates a new point cloud which is a copy from PointCloudIn, but with possibly different cvbdatatype_t and number of components. More... | |
| cvbres_t | CVC3DCreateScaledPointCloud (CVCOMPOSITE PointCloudIn, CVC3DFactors Factors, CVCOMPOSITE &PointCloudOut) |
| Creates a new point cloud with all points being scaled by the given Factors. More... | |
| cvbres_t | CVC3DCreateTransformedPointCloud (CVCOMPOSITE PointCloudIn, const CVC3DTransformation &AffineTransformation, CVCOMPOSITE &PointCloudOut) |
| Creates a new point cloud with all points being transformed by the given AffineTransformation. More... | |
| cvbres_t | CVC3DCreateTransformedPointCloudH (CVCOMPOSITE PointCloudIn, const CVC3DMatrixH Transformation, CVCOMPOSITE &PointCloudOut) |
| Creates a new point cloud with all points being transformed by the given Transformation. More... | |
| cvbres_t | CVC3DInvertMatrix (const CVC3DMatrix A, CVC3DMatrix AInv) |
| Computes the inverse of matrix A, if possible. More... | |
| cvbres_t | CVC3DInvertTransformation (const CVC3DTransformation &A, CVC3DTransformation &AInv) |
| Computes the inverse of the transformation matrix A, if possible. More... | |
| cvbres_t | CVC3DMatrixDeterminant (const CVC3DMatrix A, double &Determinant) |
| Calculates the Determinant of the given matrix A. More... | |
| cvbres_t | CVC3DMatrixFromRollPitchYawScale (double Roll, double Pitch, double Yaw, CVC3DFactors Scale, CVC3DMatrix TransformationMatrix) |
| Computes the transformation matrix M from the given Euler angles Roll, Pitch, Yaw and scaling Scale in x, y, z. More... | |
| cvbres_t | CVC3DMatrixFromRotationAnglesScale (double Alpha, double Beta, double Gamma, CVC3DFactors Scale, CVC3DMatrix TransformationMatrix) |
| Computes the transformation matrix M from the given Euler angles Alpha, Beta, Gamma and scaling Scale in x, y, z. More... | |
| cvbres_t | CVC3DMultiplyMatrices (const CVC3DMatrix A, const CVC3DMatrix B, CVC3DMatrix R) |
| Multiplies two matrices A and B. More... | |
| cvbres_t | CVC3DMultiplyTransformations (const CVC3DTransformation &A, const CVC3DTransformation &B, CVC3DTransformation &R) |
| Multiplies two transformation matrices A and B. More... | |
| cvbres_t | CVC3DRollPitchYawFromRotationMatrix (const CVC3DMatrix R, double &Roll, double &Pitch, double &Yaw) |
| Computes the Euler angles Roll, Pitch and Yaw from the given rotation matrix R. More... | |
| cvbres_t | CVC3DRollPitchYawScaleFromMatrix (const CVC3DMatrix TransformationMatrix, double &Roll, double &Pitch, double &Yaw, CVC3DFactors &Scale) |
| Computes the Euler angles Roll, Pitch, Yaw and the scaling Scale in x, y and z from the given transformation matrix TransformationMatrix. More... | |
| cvbres_t | CVC3DRollPitchYawScaleFromMatrixApproximation (const CVC3DMatrix TransformationMatrix, double &Roll, double &Pitch, double &Yaw, CVC3DFactors &Scale, double &PrecisionOfApproximation) |
| Estimates the Euler angles Roll, Pitch, Yaw and the scaling Scale in x, y and z from the given transformation matrix TransformationMatrix. The transformation matrix may be noisy. More... | |
| cvbres_t | CVC3DRotationAnglesFromRotationMatrix (const CVC3DMatrix R, double &Alpha, double &Beta, double &Gamma) |
| Computes the Euler angles Alpha, Beta and Gamma from the given rotation matrix R. More... | |
| cvbres_t | CVC3DRotationAnglesScaleFromMatrix (const CVC3DMatrix TransformationMatrix, double &Alpha, double &Beta, double &Gamma, CVC3DFactors &Scale) |
| Computes the Euler angles Alpha, Beta, Gamma and the scaling in x, y and z from the given transformation matrix TransformationMatrix. More... | |
| cvbres_t | CVC3DRotationAnglesScaleFromMatrixApproximation (const CVC3DMatrix TransformationMatrix, double &Alpha, double &Beta, double &Gamma, CVC3DFactors &Scale, double &PrecisionOfApproximation) |
| Estimates the Euler angles Alpha, Beta, Gamma and the scaling in x, y and z from the given transformation matrix TransformationMatrix. The transformation matrix may be noisy. More... | |
| cvbres_t | CVC3DRotationMatrixFromRollPitchYaw (double Roll, double Pitch, double Yaw, CVC3DMatrix R) |
| Computes the rotation matrix R from the given Euler angles Roll, Pitch and Yaw. More... | |
| cvbres_t | CVC3DRotationMatrixFromRotationAngles (double Alpha, double Beta, double Gamma, CVC3DMatrix R) |
| Computes the rotation matrix R from the given Euler angles Alpha, Beta and Gamma. More... | |
| cvbres_t | CVC3DTransformationDeterminant (const CVC3DTransformation &A, double &Determinant) |
| Calculates the Determinant of the given transformation matrix A. More... | |
| cvbres_t | CVC3DTransformPointCloud (CVCOMPOSITE PointCloudIn, const CVC3DTransformation &AffineTransformation, CVCOMPOSITE PointCloudOut) |
| Transforms all points in PointCloudIn by the given AffineTransformation and stores them in PointCloudOut. More... | |
| cvbres_t | CVC3DTransformPointCloudH (CVCOMPOSITE PointCloudIn, const CVC3DMatrixH Transformation, CVCOMPOSITE PointCloudOut) |
| Transforms all points in PointCloudIn by the given Transformation and stores them in PointCloudOut. More... | |
Functions to create new PointCloud objects by transforming their points.
| CVC3DMatrix |
Row-major 3x3 matrix.
This matrix is used e.g. in CVC3DTransformation for e.g. scaling or rotation.
| CVC3DMatrixH |
Row-major 4x4 matrix.
This matrix is used e.g. in CVC3DTransformPointCloudH for general homography transformation including perspective (pinhole camera model).
| CVC3DVector |
x, y, z vector.
This vector is used e.g. in CVC3DTransformation for translations.
| cvbres_t CVC3DAlignToXYPlane | ( | const CVC3DPlane & | Plane, |
| CVC3DTransformation & | Transformation | ||
| ) |
Calculates a rigid body transformation that maps a specified plane into the xy plane of the global coordinate system.
If a point cloud contains a tilted plane (e.g. representing a conveyer belt), which is not aligned to the xy plane, the following steps should be taken:
Please note the following:
| [in] | Plane | Plane to be aligned. |
| [out] | Transformation | Calculated transformation to move given plane to xy plane. |
| cvbres_t CVC3DCreateConvertedPointCloud | ( | CVCOMPOSITE | PointCloudIn, |
| cvbval_t | Flags, | ||
| CVCOMPOSITE & | PointCloudOut | ||
| ) |
Creates a new point cloud which is a copy from PointCloudIn, but with possibly different cvbdatatype_t and number of components.
The given PointCloudIn must have a valid CVC3DPointCloudLayout.
| [in] | PointCloudIn | Handle to point cloud object to convert. |
| [in] | Flags | CVC3DPointCloudFlags specifying the kind of point cloud to be created. |
| [out] | PointCloudOut | Variable to receive the handle of the resulting point cloud. |
| cvbres_t CVC3DCreateScaledPointCloud | ( | CVCOMPOSITE | PointCloudIn, |
| CVC3DFactors | Factors, | ||
| CVCOMPOSITE & | PointCloudOut | ||
| ) |
Creates a new point cloud with all points being scaled by the given Factors.
The given PointCloudIn must have a valid CVC3DPointCloudLayout.
| [in] | PointCloudIn | Handle to point cloud object to scale. |
| [in] | Factors | Scale factors to be applied to each point. |
| [out] | PointCloudOut | Variable to receive the scaled point cloud. |
NaN.| cvbres_t CVC3DCreateTransformedPointCloud | ( | CVCOMPOSITE | PointCloudIn, |
| const CVC3DTransformation & | AffineTransformation, | ||
| CVCOMPOSITE & | PointCloudOut | ||
| ) |
Creates a new point cloud with all points being transformed by the given AffineTransformation.
The given PointCloudIn must have a valid CVC3DPointCloudLayout.
| [in] | PointCloudIn | Handle to point cloud object to be transformed. |
| [in] | AffineTransformation | Homogeneous transformation matrix. |
| [out] | PointCloudOut | Variable to receive the transformed point cloud. |
NaN.| cvbres_t CVC3DCreateTransformedPointCloudH | ( | CVCOMPOSITE | PointCloudIn, |
| const CVC3DMatrixH | Transformation, | ||
| CVCOMPOSITE & | PointCloudOut | ||
| ) |
Creates a new point cloud with all points being transformed by the given Transformation.
The given PointCloudIn must have a valid CVC3DPointCloudLayout.
| [in] | PointCloudIn | Handle to point cloud object to be transformed. |
| [in] | Transformation | Homogeneous transformation matrix. |
| [out] | PointCloudOut | Variable to receive the transformed point cloud. |
NaN or is nullptr.| cvbres_t CVC3DInvertMatrix | ( | const CVC3DMatrix | A, |
| CVC3DMatrix | AInv | ||
| ) |
Computes the inverse of matrix A, if possible.
Inversion is possible if the determinant is not zero.
| [in] | A | Input matrix. |
| [out] | AInv | Matrix to be filled with the coefficients of the inverted matrix A. |
| cvbres_t CVC3DInvertTransformation | ( | const CVC3DTransformation & | A, |
| CVC3DTransformation & | AInv | ||
| ) |
Computes the inverse of the transformation matrix A, if possible.
Inversion is possible if the determinant is not zero.
| [in] | A | Input transformation. |
| [out] | AInv | Transformation matrix to be filled with the coefficients of the inverted A. |
| cvbres_t CVC3DMatrixDeterminant | ( | const CVC3DMatrix | A, |
| double & | Determinant | ||
| ) |
Calculates the Determinant of the given matrix A.
| [in] | A | Matrix for which the Determinant is to be calculated. |
| [out] | Determinant | Variable to be filled with the determinant. |
| cvbres_t CVC3DMatrixFromRollPitchYawScale | ( | double | Roll, |
| double | Pitch, | ||
| double | Yaw, | ||
| CVC3DFactors | Scale, | ||
| CVC3DMatrix | TransformationMatrix | ||
| ) |
Computes the transformation matrix M from the given Euler angles Roll, Pitch, Yaw and scaling Scale in x, y, z.
This function computes the transformation matrix after the z-y′-x″ convention (see https://en.wikipedia.org/wiki/Euler_angles).
The scaling is applied before rotation:
M = R_z*R_y*R_x*S*xyz
where R_x, R_y, R_z is the rotation around x, y, z
S is the scaling matrix
| [in] | Roll | Angle around _x_″ in degrees. |
| [in] | Pitch | Angle around _y_′ axis in degrees. |
| [in] | Yaw | Angle around z axis in degrees. |
| [in] | Scale | Scaling factors in x, y and z. |
| [out] | TransformationMatrix | Non-nullptr pointer to matrix to be filled with the rotation matrix elements. |
| cvbres_t CVC3DMatrixFromRotationAnglesScale | ( | double | Alpha, |
| double | Beta, | ||
| double | Gamma, | ||
| CVC3DFactors | Scale, | ||
| CVC3DMatrix | TransformationMatrix | ||
| ) |
Computes the transformation matrix M from the given Euler angles Alpha, Beta, Gamma and scaling Scale in x, y, z.
The scaling is applied before rotation:
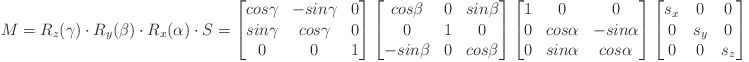
where
Alpha, Beta, Gamma are the rotation angles around x, y, z
sx, sy, sz are the scaling factors for x, y, z.
| [in] | Alpha | Angle around x axis in degrees. |
| [in] | Beta | Angle around y axis in degrees. |
| [in] | Gamma | Angle around z axis in degrees. |
| [in] | Scale | Scaling factors in x, y and z. |
| [out] | TransformationMatrix | Non-nullptr pointer to matrix to be filled with the rotation matrix elements. |
| cvbres_t CVC3DMultiplyMatrices | ( | const CVC3DMatrix | A, |
| const CVC3DMatrix | B, | ||
| CVC3DMatrix | R | ||
| ) |
Multiplies two matrices A and B.
| [in] | A | Left hand side matrix. |
| [in] | B | Right hand side matrix. |
| [out] | R | Matrix to be filled with the result coefficients of the operation. |
| cvbres_t CVC3DMultiplyTransformations | ( | const CVC3DTransformation & | A, |
| const CVC3DTransformation & | B, | ||
| CVC3DTransformation & | R | ||
| ) |
Multiplies two transformation matrices A and B.
| [in] | A | Left hand side transformation. |
| [in] | B | Right hand side transformation. |
| [out] | R | Transformation to be filled with the result coefficients of the operation. |
| cvbres_t CVC3DRollPitchYawFromRotationMatrix | ( | const CVC3DMatrix | R, |
| double & | Roll, | ||
| double & | Pitch, | ||
| double & | Yaw | ||
| ) |
Computes the Euler angles Roll, Pitch and Yaw from the given rotation matrix R.
This function computes the rotation matrix after the z-y′-x″ convention (see https://en.wikipedia.org/wiki/Euler_angles).
| [in] | R | Non-nullptr pointer to rotation matrix elements. |
| [out] | Roll | Variable to receive angle around _x_″ in degrees. |
| [out] | Pitch | Variable to receive angle around _y_′ axis in degrees. |
| [out] | Yaw | Variable to receive angle around z axis in degrees. |
| cvbres_t CVC3DRollPitchYawScaleFromMatrix | ( | const CVC3DMatrix | TransformationMatrix, |
| double & | Roll, | ||
| double & | Pitch, | ||
| double & | Yaw, | ||
| CVC3DFactors & | Scale | ||
| ) |
Computes the Euler angles Roll, Pitch, Yaw and the scaling Scale in x, y and z from the given transformation matrix TransformationMatrix.
This function computes the rotation matrix after the z-y′-x″ convention (see https://en.wikipedia.org/wiki/Euler_angles).
The scaling must be applied before rotation:
M = R_z*R_y*R_x*S
where R_x, R_y, R_z is the rotation around x, y, z
S is the scaling matrix
The scaling factors are computed from the normed matrix TransformationMatrix and threfore positive as a start. If the determinant of the normed matrix is -1, the scaling factor in z is set to a negative value.
| [in] | TransformationMatrix | Non-nullptr pointer to transformation matrix elements. |
| [out] | Roll | Variable to receive angle around _x_″ in degrees. |
| [out] | Pitch | Variable to receive angle around _y_′ axis in degrees. |
| [out] | Yaw | Variable to receive angle around z axis in degrees. |
| [out] | Scale | Scaling factors in x, y and z. |
| cvbres_t CVC3DRollPitchYawScaleFromMatrixApproximation | ( | const CVC3DMatrix | TransformationMatrix, |
| double & | Roll, | ||
| double & | Pitch, | ||
| double & | Yaw, | ||
| CVC3DFactors & | Scale, | ||
| double & | PrecisionOfApproximation | ||
| ) |
Estimates the Euler angles Roll, Pitch, Yaw and the scaling Scale in x, y and z from the given transformation matrix TransformationMatrix. The transformation matrix may be noisy.
This function computes the rotation matrix after the z-y′-x″ convention (see https://en.wikipedia.org/wiki/Euler_angles).
The scaling must be applied before rotation:
M = R_z*R_y*R_x*S
where R_x, R_y, R_z is the rotation around x, y, z
S is the scaling matrix
This function should be used, if the matrix is noisy or not a valid transformation matrix.
Rotation angles and scaling factors are estimated using the Nelder-Mead algorithm. Therefore a cost function is set up and minimized over several iterations. The minimum value after the iteration stopped is stored to PrecisionOfApproximation. If the given matrix is valid and not noisy, the PrecisionOfApproximation will be very low.
| [in] | TransformationMatrix | Non-nullptr pointer to transformation matrix elements. |
| [out] | Roll | Variable to receive angle around _x_″ in degrees. |
| [out] | Pitch | Variable to receive angle around _y_′ axis in degrees. |
| [out] | Yaw | Variable to receive angle around z axis in degrees. |
| [out] | Scale | Scaling factors in x, y and z. |
| [out] | PrecisionOfApproximation | Precision of the approximation. |
| cvbres_t CVC3DRotationAnglesFromRotationMatrix | ( | const CVC3DMatrix | R, |
| double & | Alpha, | ||
| double & | Beta, | ||
| double & | Gamma | ||
| ) |
Computes the Euler angles Alpha, Beta and Gamma from the given rotation matrix R.
The rotation matrix R is interpreted as:

where
Alpha, Beta, Gamma are the rotation angles around x, y, z.
| [in] | R | Non-nullptr pointer to rotation matrix elements. |
| [out] | Alpha | Variable to receive rotation angle around x axis in degrees. |
| [out] | Beta | Variable to receive rotation angle around y axis in degrees. |
| [out] | Gamma | Variable to receive rotation angle around z axis in degrees. |
| cvbres_t CVC3DRotationAnglesScaleFromMatrix | ( | const CVC3DMatrix | TransformationMatrix, |
| double & | Alpha, | ||
| double & | Beta, | ||
| double & | Gamma, | ||
| CVC3DFactors & | Scale | ||
| ) |
Computes the Euler angles Alpha, Beta, Gamma and the scaling in x, y and z from the given transformation matrix TransformationMatrix.
The transformation matrix M is interpreted as:
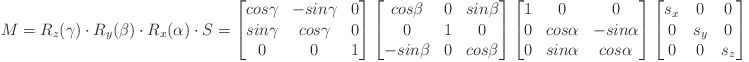
where
Alpha, Beta, Gamma are the rotation angles around x, y, z
sx, sy, sz are the scaling factors for x, y, z.
The scaling factors are computed from the normed matrix TransformationMatrix and threfore positive as a start. If the determinant of the normed matrix is -1, the scaling factor in z is set to a negative value.
| [in] | TransformationMatrix | Non-nullptr pointer to transformation matrix elements. |
| [out] | Alpha | Variable to receive rotation angle around x axis in degrees. |
| [out] | Beta | Variable to receive rotation angle around y axis in degrees. |
| [out] | Gamma | Variable to receive rotation angle around z axis in degrees. |
| [out] | Scale | Scaling factors in x, y and z. |
| cvbres_t CVC3DRotationAnglesScaleFromMatrixApproximation | ( | const CVC3DMatrix | TransformationMatrix, |
| double & | Alpha, | ||
| double & | Beta, | ||
| double & | Gamma, | ||
| CVC3DFactors & | Scale, | ||
| double & | PrecisionOfApproximation | ||
| ) |
Estimates the Euler angles Alpha, Beta, Gamma and the scaling in x, y and z from the given transformation matrix TransformationMatrix. The transformation matrix may be noisy.
The transformation matrix M is interpreted as:
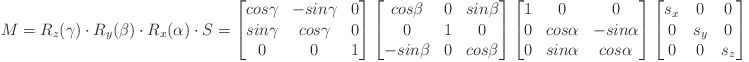
where
Alpha, Beta, Gamma are the rotation angles around x, y, z
sx, sy, sz are the scaling factors for x, y, z.
This function should be used, if the matrix is noisy or not a valid transformation matrix.
Rotation angles and scaling factors are estimated using the Nelder-Mead algorithm. Therefore a cost function is set up and minimized over several iterations. The minimum value after the iteration stopped is stored to PrecisionOfApproximation. If the given matrix is valid and not noisy, the PrecisionOfApproximation will be very low.
| [in] | TransformationMatrix | Non-nullptr pointer to transformation matrix elements. |
| [out] | Alpha | Variable to receive rotation angle around x axis in degrees. |
| [out] | Beta | Variable to receive rotation angle around y axis in degrees. |
| [out] | Gamma | Variable to receive rotation angle around z axis in degrees. |
| [out] | Scale | Scaling factors in x, y and z. |
| [out] | PrecisionOfApproximation | Precision of the approximation. |
| cvbres_t CVC3DRotationMatrixFromRollPitchYaw | ( | double | Roll, |
| double | Pitch, | ||
| double | Yaw, | ||
| CVC3DMatrix | R | ||
| ) |
Computes the rotation matrix R from the given Euler angles Roll, Pitch and Yaw.
This function computes the rotation matrix after the z-y′-x″ convention (see https://en.wikipedia.org/wiki/Euler_angles).
| [in] | Roll | Angle around _x_″ in degrees. |
| [in] | Pitch | Angle around _y_′ axis in degrees. |
| [in] | Yaw | Angle around z axis in degrees. |
| [out] | R | Non-nullptr pointer to matrix to be filled with the rotation matrix elements. |
| cvbres_t CVC3DRotationMatrixFromRotationAngles | ( | double | Alpha, |
| double | Beta, | ||
| double | Gamma, | ||
| CVC3DMatrix | R | ||
| ) |
Computes the rotation matrix R from the given Euler angles Alpha, Beta and Gamma.
The rotation matrix R is computed via:

where
Alpha, Beta, Gamma are the rotation angles around x, y, z.
| [in] | Alpha | Angle around x axis in degrees. |
| [in] | Beta | Angle around y axis in degrees. |
| [in] | Gamma | Angle around z axis in degrees. |
| [out] | R | Non-nullptr pointer to matrix to be filled with the rotation matrix elements. |
| cvbres_t CVC3DTransformationDeterminant | ( | const CVC3DTransformation & | A, |
| double & | Determinant | ||
| ) |
| cvbres_t CVC3DTransformPointCloud | ( | CVCOMPOSITE | PointCloudIn, |
| const CVC3DTransformation & | AffineTransformation, | ||
| CVCOMPOSITE | PointCloudOut | ||
| ) |
Transforms all points in PointCloudIn by the given AffineTransformation and stores them in PointCloudOut.
The given PointCloudIn and PointCloudOut must have valid CVC3DPointCloudLayout.
| [in] | PointCloudIn | Handle to point cloud object to be transformed. |
| [in] | AffineTransformation | Homogeneous transformation matrix. |
| [in] | PointCloudOut | Handle to sparse point cloud were the transformed points are stored in. |
NaN.| cvbres_t CVC3DTransformPointCloudH | ( | CVCOMPOSITE | PointCloudIn, |
| const CVC3DMatrixH | Transformation, | ||
| CVCOMPOSITE | PointCloudOut | ||
| ) |
Transforms all points in PointCloudIn by the given Transformation and stores them in PointCloudOut.
The given PointCloudIn and PointCloudOut must have valid CVC3DPointCloudLayout.
| [in] | PointCloudIn | Handle to point cloud object to be transformed. |
| [in] | Transformation | Homogeneous transformation matrix. |
| [in] | PointCloudOut | Handle to sparse point cloud were the transformed points are stored in. |
NaN or is nullptr.