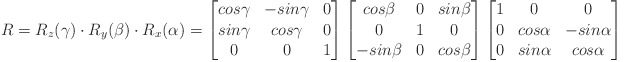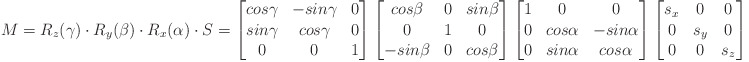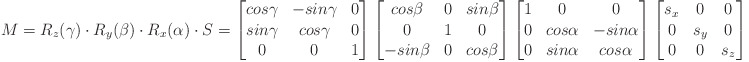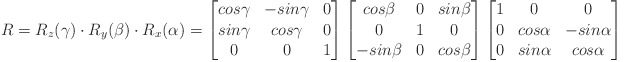Double precision 3x3 matrix class. More...

#include <cvb/matrix_3d.hpp>

Public Member Functions
	Matrix3D () noexcept=default
	Default constructor for empty matrix. More...

template<std::size_t N>
	Matrix3D (const double(&list)[N]) noexcept
	Construct a 3x3 matrix with an initializer list. More...

	Matrix3D (double alpha, double beta, double gamma)
	Creates a rotation matrix from the given Euler angles. More...

	Matrix3D (double alpha, double beta, double gamma, Factors3D scale)
	Creates a transformation matrix from the given Euler angles and scaling. More...

bool	TryGetRotationAngles (double &alpha, double &beta, double &gamma) const noexcept
	Tries to compute the Euler angles from the matrix. More...

void	RotationAnglesScale (double &alpha, double &beta, double &gamma, Factors3D &scale, double &precision) const
	Computes the Euler angles and scaling from the matrix. More...

void	RollPitchYaw (double &roll, double &pitch, double &yaw) const
	Computes the Euler angles Roll, Pitch and Yaw for this matrix. More...

const double *	operator[] (int row) const noexcept
	Index based element access. More...

double *	operator[] (int row) noexcept
	Index based element access. More...

const double &	At (int row, int column) const noexcept
	Index based element access. More...

double &	At (int row, int column) noexcept
	Index based element access. More...

double	Det () const
	Matrix determinant. More...

void	Invert ()
	Inverts this matrix in-place if possible. More...

Matrix3D	Inverse ()
	Gets the inverse of this matrix if possible. More...

bool	operator== (const Matrix3D &matrix) const noexcept
	Compares to an other matrix. More...

bool	operator!= (const Matrix3D &matrix) const noexcept
	Compares to an other matrix. More...

Matrix3D &	operator+= (const Matrix3D &matrix) noexcept
	Adds and assigns to this matrix. More...

Matrix3D &	operator-= (const Matrix3D &matrix) noexcept
	Subtracts and assigns to this matrix. More...

Matrix3D &	operator*= (const Matrix3D &matrix)
	Multiplies and assigns to this matrix. More...

Matrix3D &	operator*= (const double &value) noexcept
	Multiplies and assigns to this matrix. More...

Matrix3D &	operator/= (const double &value) noexcept
	Divides each element of this matrix by the given value. More...

Static Public Member Functions
static Matrix3D	Identity () noexcept
	The identity element. More...

Related Functions
(Note that these are not member functions.)
Matrix3D	operator+ (const Matrix3D &lhs, const Matrix3D &rhs)
	Add two matrices. More...

Matrix3D	operator- (const Matrix3D &lhs, const Matrix3D &rhs)
	Subtract two matrices. More...

Matrix3D	operator* (const Matrix3D &lhs, const Matrix3D &rhs)
	Multiply two matrices. More...

Point3D< double >	operator* (const Matrix3D &lhs, const Point3D< double > &rhs)
	Multiply matrix with 3D point. More...

Matrix3D	operator* (const Matrix3D &lhs, const double &rhs)
	Multiply matrix with scalar. More...

Matrix3D	operator* (const double &lhs, const Matrix3D &rhs)
	Multiply scalar with matrix . More...

Matrix3D	operator/ (const Matrix3D &lhs, const double &rhs)
	Divide matrix by scalar. More...

Detailed Description

Double precision 3x3 matrix class.

Constructor & Destructor Documentation

◆ Matrix3D() [1/4]

Matrix3D ( )

defaultnoexcept

Default constructor for empty matrix.

Exceptions

Does	not throw any exception.

◆ Matrix3D() [2/4]

Matrix3D ( const double(&) list[N] )

inlinenoexcept

Construct a 3x3 matrix with an initializer list.

Parameters

[in] list Containing exactly 9 elements.

Exceptions

Does	not throw any exception.

◆ Matrix3D() [3/4]

Matrix3D	(	double	alpha,
		double	beta,
		double	gamma
	)

inline

Creates a rotation matrix from the given Euler angles.

The rotation matrix R is computed via:

where
alpha, beta, gamma are the rotation angles around x, y, z.

Parameters

[in]	alpha	Angle around x axis in degrees.
[in]	beta	Angle around y axis in degrees.
[in]	gamma	Angle around z axis in degrees.

Exceptions

Any	exception derived from std::exception including CvbException.

◆ Matrix3D() [4/4]

Matrix3D	(	double	alpha,
		double	beta,
		double	gamma,
		Factors3D	scale
	)

inline

Creates a transformation matrix from the given Euler angles and scaling.

Note, that the scaling is applied before rotation:

where
alpha, beta, gamma are the rotation angles around x, y, z.
s_x, s_y, s_z are the scaling factors for x, y, z.

Parameters

[in]	alpha	Angle around x axis in degrees.
[in]	beta	Angle around y axis in degrees.
[in]	gamma	Angle around z axis in degrees.
[in]	scale	Scaling factors in x, y and z.

Exceptions

Any	exception derived from std::exception including CvbException.

Member Function Documentation

◆ At() [1/2]

const double & At	(	int	row,
		int	column
	)		const

inlinenoexcept

Index based element access.

Parameters

[in]	row	The row to access.
[in]	column	The column to access.

Returns: The matrix element.

Exceptions

Does	not throw any exception.

◆ At() [2/2]

double & At	(	int	row,
		int	column
	)

inlinenoexcept

Index based element access.

Parameters

[in]	row	The row to access.
[in]	column	The column to access.

Returns: The matrix element.

Exceptions

Does	not throw any exception.

◆ Det()

double Det ( ) const

inline

Matrix determinant.

Returns: The determinant.

Exceptions

Any	exception derived from std::exception including CvbException.

◆ Identity()

static Matrix3D Identity ( )

inlinestaticnoexcept

The identity element.

Returns: An identity matrix.

Exceptions

Does	not throw any exception.

◆ Inverse()

Matrix3D Inverse ( )

inline

Gets the inverse of this matrix if possible.

Exceptions

Any	exception derived from std::exception including CvbException.

Returns: Inverse.

Might cause division by zero.

◆ Invert()

void Invert ( )

inline

Inverts this matrix in-place if possible.

Exceptions

Any	exception derived from std::exception including CvbException.

Might cause division by zero.

◆ operator!=()

bool operator!= ( const Matrix3D & matrix ) const

inlinenoexcept

Compares to an other matrix.

Parameters

[in] matrix Other matrix.

Returns: True if not equal, otherwise false.

Exceptions

Does	not throw any exception.

◆ operator*=() [1/2]

Matrix3D & operator*= ( const double & value )

inlinenoexcept

Multiplies and assigns to this matrix.

Parameters

[in] value Factor.

Returns: This matrix.

Exceptions

Does	not throw any exception.

◆ operator*=() [2/2]

Matrix3D & operator*= ( const Matrix3D & matrix )

inline

Multiplies and assigns to this matrix.

Parameters

[in] matrix Other matrix.

Returns: This matrix.

Exceptions

Any	exception derived from std::exception including CvbException.

◆ operator+=()

Matrix3D & operator+= ( const Matrix3D & matrix )

inlinenoexcept

Adds and assigns to this matrix.

Parameters

[in] matrix Other matrix.

Returns: This matrix.

Exceptions

Does	not throw any exception.

◆ operator-=()

Matrix3D & operator-= ( const Matrix3D & matrix )

inlinenoexcept

Subtracts and assigns to this matrix.

Parameters

[in] matrix Other matrix.

Returns: This matrix.

Exceptions

Does	not throw any exception.

◆ operator/=()

Matrix3D & operator/= ( const double & value )

inlinenoexcept

Divides each element of this matrix by the given value.

Parameters

[in] value Divisor.

Returns: This matrix.

Exceptions

Does	not throw any exception.

◆ operator==()

bool operator== ( const Matrix3D & matrix ) const

inlinenoexcept

Compares to an other matrix.

Parameters

[in] matrix Other matrix.

Returns: True if equal, otherwise false.

Exceptions

Does	not throw any exception.

◆ operator[]() [1/2]

const double * operator[] ( int row ) const

inlinenoexcept

Index based element access.

Parameters

[in] row

Returns: A raw pointer to the row

Exceptions

Does	not throw any exception.

◆ operator[]() [2/2]

double * operator[] ( int row )

inlinenoexcept

Index based element access.

Parameters

[in] row

Returns: A raw pointer to the row

Exceptions

Does	not throw any exception.

◆ RollPitchYaw()

void RollPitchYaw	(	double &	roll,
		double &	pitch,
		double &	yaw
	)		const

inline

Computes the Euler angles Roll, Pitch and Yaw for this matrix.

This function assumes the rotation matrix defined after the z-y′-x″ convention (see https://en.wikipedia.org/wiki/Euler_angles). The rotation matrix is interpreted as:

R = R_z*R_y*R_x
where R_x, R_y, R_z is the rotation around x″, y′, z.

Parameters

[in]	roll	Variable to receive angle around x″ in degrees.
[in]	pitch	Variable to receive angle around y′ in degrees.
[in]	yaw	Variable to receive angle around z axis in degrees.

Exceptions

Any	exception derived from std::exception including CvbException.

Note: If the resulting pitch is outside the range ]-90° .. 90°[, the computation of the Euler angles is ambiguous (rotation direction may be inversed).

◆ RotationAnglesScale()

void RotationAnglesScale	(	double &	alpha,
		double &	beta,
		double &	gamma,
		Factors3D &	scale,
		double &	precision
	)		const

inline

Computes the Euler angles and scaling from the matrix.

The transformation matrix M is interpreted as:

where
alpha, beta, gamma are the rotation angles around x, y, z.
s_x, s_y, s_z are the scaling factors for x, y, z.

If the matrix only contains rotation and scaling, i.e. it is not noisy, then the scaling factors are computed from the normed matrix and threfore positive as a start. If the determinant of the normed matrix is -1, the scaling factor in z is set to a negative value.

If calculating the rotation and scaling from the matrix without approximation is successful the precision value is set to -1. Otherwise an approximation is calculated. This is the case for non-valid rotation matrices (e.g. due to noise). Then the rotation angles and scaling factors are estimated using the Nelder-Mead algorithm. Therefore a cost function is set up and minimized over several iterations. The minimum value after the iteration stopped is stored to precision. If the given matrix is valid and not noisy, the precision will be very low. Note, that this estimation does not work for large scaling factors or if all scaling factors are negative. In this case the output precision will be large (in general greater 1). Then please norm your matrix first by dividing all matrix elements by a matrix norm (e.g. the Frobenius norm or other).

Note: If one of the resulting angles is outside the range ]-90° .. 90°[ or one of the scaling factors is negative, the computation of the Euler angles and the scaling factors is ambiguous (rotation direction may be inversed, negative scaling is the same as rotation about 180 degree).

Parameters

[out]	alpha	Variable to receive rotation angle around x axis in degrees.
[out]	beta	Variable to receive rotation angle around y axis in degrees.
[out]	gamma	Variable to receive rotation angle around z axis in degrees.
[out]	scale	Scaling factors in x, y and z.
[out]	precision	Precision of approximation. if results are calculated directly without approximation, this value is -1.

Exceptions

Any	exception derived from std::exception including CvbException.

◆ TryGetRotationAngles()

bool TryGetRotationAngles	(	double &	alpha,
		double &	beta,
		double &	gamma
	)		const

inlinenoexcept

Tries to compute the Euler angles from the matrix.

The matrix is interpreted as a rotation matrix R:

where
alpha, beta, gamma are the rotation angles around x, y, z.

Note: If the resulting beta is outside the range ]-90° .. 90°[ , the computation of the Euler angles is ambiguous (rotation direction may be inversed).

Parameters

[out]	alpha	Variable to receive rotation angle around x axis in degrees.
[out]	beta	Variable to receive rotation angle around y axis in degrees.
[out]	gamma	Variable to receive rotation angle around z axis in degrees.

Returns: False, if matrix is not a valid rotation matrix and angles cannot be calculated. Otherwise true.

Friends And Related Function Documentation

◆ operator*() [1/4]

Matrix3D operator*	(	const double &	lhs,
		const Matrix3D &	rhs
	)

Parameters

[in]	lhs	Right hand side value.
[in]	rhs	Left hand side matrix.

Returns: The computation result.

Exceptions

Does	not throw any exception.

◆ operator*() [2/4]

Matrix3D operator*	(	const Matrix3D &	lhs,
		const double &	rhs
	)

Parameters

[in]	lhs	Right hand side matrix.
[in]	rhs	Left hand side value.

Returns: The computation result.

Exceptions

Does	not throw any exception.

◆ operator*() [3/4]

Matrix3D operator*	(	const Matrix3D &	lhs,
		const Matrix3D &	rhs
	)

Parameters

[in]	lhs	Right hand side matrix.
[in]	rhs	Left hand side matrix.

Returns: The computation result.

Exceptions

Any	exception derived from std::exception including CvbException.

◆ operator*() [4/4]

Point3D< double > operator*	(	const Matrix3D &	lhs,
		const Point3D< double > &	rhs
	)

Parameters

[in]	lhs	Right hand side matrix.
[in]	rhs	Left hand side point.

Returns: The computation result.

Exceptions

Does	not throw any exception.

◆ operator+()

Matrix3D operator+	(	const Matrix3D &	lhs,
		const Matrix3D &	rhs
	)

Parameters

[in]	lhs	Right hand side matrix.
[in]	rhs	Left hand side matrix.

Returns: The computation result.

Exceptions

Does	not throw any exception.

◆ operator-()

Matrix3D operator-	(	const Matrix3D &	lhs,
		const Matrix3D &	rhs
	)

Parameters

[in]	lhs	Right hand side matrix.
[in]	rhs	Left hand side matrix.

Returns: The computation result.

Exceptions

Does	not throw any exception.

◆ operator/()

Matrix3D operator/	(	const Matrix3D &	lhs,
		const double &	rhs
	)

Parameters

[in]	lhs	Right hand side matrix.
[in]	rhs	Left hand side value.

Returns: The computation result.

Exceptions

Does	not throw any exception.

Public Member Functions

Static Public Member Functions

Related Functions

Detailed Description

Constructor & Destructor Documentation

◆ Matrix3D() [1/4]

◆ Matrix3D() [2/4]

◆ Matrix3D() [3/4]

◆ Matrix3D() [4/4]

Member Function Documentation

◆ At() [1/2]

◆ At() [2/2]

◆ Det()

◆ Identity()

◆ Inverse()

◆ Invert()

◆ operator!=()

◆ operator*=() [1/2]

◆ operator*=() [2/2]

◆ operator+=()

◆ operator-=()

◆ operator/=()

◆ operator==()

◆ operator[]() [1/2]

◆ operator[]() [2/2]

◆ RollPitchYaw()

◆ RotationAnglesScale()

◆ TryGetRotationAngles()

Friends And Related Function Documentation

◆ operator*() [1/4]

◆ operator*() [2/4]

◆ operator*() [3/4]

◆ operator*() [4/4]

◆ operator+()

◆ operator-()

◆ operator/()