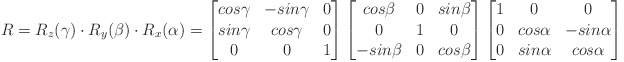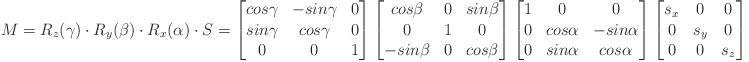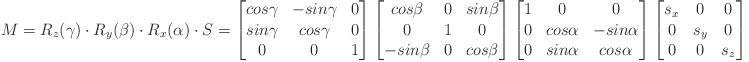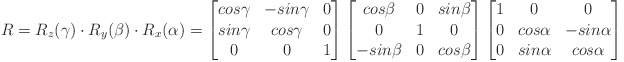|
| | Matrix3D () noexcept=default |
| | Default constructor for empty matrix.
|
| |
| template<std::size_t N> |
| | Matrix3D (const double(&list)[N]) noexcept |
| | Construct a 3x3 matrix with an initializer list.
|
| |
| | Matrix3D (double alpha, double beta, double gamma) |
| | Creates a rotation matrix from the given Euler angles.
|
| |
| | Matrix3D (double alpha, double beta, double gamma, Factors3D scale) |
| | Creates a transformation matrix from the given Euler angles and scaling.
|
| |
| bool | TryGetRotationAngles (double &alpha, double &beta, double &gamma) const noexcept |
| | Tries to compute the Euler angles from the matrix.
|
| |
| void | RotationAnglesScale (double &alpha, double &beta, double &gamma, Factors3D &scale, double &precision) const |
| | Computes the Euler angles and scaling from the matrix.
|
| |
| void | RollPitchYaw (double &roll, double &pitch, double &yaw) const |
| | Computes the Euler angles Roll, Pitch and Yaw for this matrix.
|
| |
| const double * | operator[] (int row) const noexcept |
| | Index based element access.
|
| |
| double * | operator[] (int row) noexcept |
| | Index based element access.
|
| |
| const double & | At (int row, int column) const noexcept |
| | Index based element access.
|
| |
| double & | At (int row, int column) noexcept |
| | Index based element access.
|
| |
| double | Det () const |
| | Matrix determinant.
|
| |
| void | Invert () |
| | Inverts this matrix in-place if possible.
|
| |
| Matrix3D | Inverse () |
| | Gets the inverse of this matrix if possible.
|
| |
| bool | operator== (const Matrix3D &matrix) const noexcept |
| | Compares to an other matrix.
|
| |
| bool | operator!= (const Matrix3D &matrix) const noexcept |
| | Compares to an other matrix.
|
| |
| Matrix3D & | operator+= (const Matrix3D &matrix) noexcept |
| | Adds and assigns to this matrix.
|
| |
| Matrix3D & | operator-= (const Matrix3D &matrix) noexcept |
| | Subtracts and assigns to this matrix.
|
| |
| Matrix3D & | operator*= (const Matrix3D &matrix) |
| | Multiplies and assigns to this matrix.
|
| |
| Matrix3D & | operator*= (const double &value) noexcept |
| | Multiplies and assigns to this matrix.
|
| |
| Matrix3D & | operator/= (const double &value) noexcept |
| | Divides each element of this matrix by the given value.
|
| |
Double precision 3x3 matrix class.
Creates a transformation matrix from the given Euler angles and scaling.
Note, that the scaling is applied before rotation:
where
alpha, beta, gamma are the rotation angles around x, y, z.
sx, sy, sz are the scaling factors for x, y, z.
- Parameters
-
| [in] | alpha | Angle around x axis in degrees. |
| [in] | beta | Angle around y axis in degrees. |
| [in] | gamma | Angle around z axis in degrees. |
| [in] | scale | Scaling factors in x, y and z. |
- Exceptions
-
| void RollPitchYaw |
( |
double & | roll, |
|
|
double & | pitch, |
|
|
double & | yaw ) const |
|
inline |
Computes the Euler angles Roll, Pitch and Yaw for this matrix.
This function assumes the rotation matrix defined after the z-y′-x″ convention (see https://en.wikipedia.org/wiki/Euler_angles). The rotation matrix is interpreted as:
R = R_z*R_y*R_x
where R_x, R_y, R_z is the rotation around x″, y′, z.
- Parameters
-
| [in] | roll | Variable to receive angle around x″ in degrees. |
| [in] | pitch | Variable to receive angle around y′ in degrees. |
| [in] | yaw | Variable to receive angle around z axis in degrees. |
- Exceptions
-
- Note
- If the resulting pitch is outside the range ]-90° .. 90°[, the computation of the Euler angles is ambiguous (rotation direction may be inversed).
| void RotationAnglesScale |
( |
double & | alpha, |
|
|
double & | beta, |
|
|
double & | gamma, |
|
|
Factors3D & | scale, |
|
|
double & | precision ) const |
|
inline |
Computes the Euler angles and scaling from the matrix.
The transformation matrix M is interpreted as:
where
alpha, beta, gamma are the rotation angles around x, y, z.
sx, sy, sz are the scaling factors for x, y, z.
If the matrix only contains rotation and scaling, i.e. it is not noisy, then the scaling factors are computed from the normed matrix and threfore positive as a start. If the determinant of the normed matrix is -1, the scaling factor in z is set to a negative value.
If calculating the rotation and scaling from the matrix without approximation is successful the precision value is set to -1. Otherwise an approximation is calculated. This is the case for non-valid rotation matrices (e.g. due to noise). Then the rotation angles and scaling factors are estimated using the Nelder-Mead algorithm. Therefore a cost function is set up and minimized over several iterations. The minimum value after the iteration stopped is stored to precision. If the given matrix is valid and not noisy, the precision will be very low. Note, that this estimation does not work for large scaling factors or if all scaling factors are negative. In this case the output precision will be large (in general greater 1). Then please norm your matrix first by dividing all matrix elements by a matrix norm (e.g. the Frobenius norm or other).
- Note
- If one of the resulting angles is outside the range ]-90° .. 90°[ or one of the scaling factors is negative, the computation of the Euler angles and the scaling factors is ambiguous (rotation direction may be inversed, negative scaling is the same as rotation about 180 degree).
- Parameters
-
| [out] | alpha | Variable to receive rotation angle around x axis in degrees. |
| [out] | beta | Variable to receive rotation angle around y axis in degrees. |
| [out] | gamma | Variable to receive rotation angle around z axis in degrees. |
| [out] | scale | Scaling factors in x, y and z. |
| [out] | precision | Precision of approximation. if results are calculated directly without approximation, this value is -1. |
- Exceptions
-
| bool TryGetRotationAngles |
( |
double & | alpha, |
|
|
double & | beta, |
|
|
double & | gamma ) const |
|
inlinenoexcept |
Tries to compute the Euler angles from the matrix.
The matrix is interpreted as a rotation matrix R:
where
alpha, beta, gamma are the rotation angles around x, y, z.
- Note
- If the resulting beta is outside the range ]-90° .. 90°[ , the computation of the Euler angles is ambiguous (rotation direction may be inversed).
- Parameters
-
| [out] | alpha | Variable to receive rotation angle around x axis in degrees. |
| [out] | beta | Variable to receive rotation angle around y axis in degrees. |
| [out] | gamma | Variable to receive rotation angle around z axis in degrees. |
- Returns
- False, if matrix is not a valid rotation matrix and angles cannot be calculated. Otherwise true.