Functions | |
| cvbres_t | ForwardWaveletTransform (IMG ImgIn, TWaveletFilter FilterType, cvbdim_t AnchorLow, cvbdim_t AnchorHigh, double LowpassFilter[], double HighpassFilter[], cvbdim_t LengthFilter, IMG &ImgApproximation, IMG &ImgDetailX, IMG &ImgDetailY, IMG &ImgDetailXY) |
| This function performs the two-dimensional wavelet decomposition on the input image. More... | |
| cvbres_t | InverseWaveletTransform (TWaveletFilter FilterType, cvbdim_t AnchorLow, cvbdim_t AnchorHigh, double LowpassFilter[], double HighpassFilter[], cvbdim_t LengthFilter, IMG ImgApproximation, IMG ImgDetailX, IMG ImgDetailY, IMG ImgDetailXY, IMG &ImgOut) |
| This function performs the two-dimensional inverse wavelet transform on the sub-images. More... | |
| cvbres_t ForwardWaveletTransform | ( | IMG | ImgIn, |
| TWaveletFilter | FilterType, | ||
| cvbdim_t | AnchorLow, | ||
| cvbdim_t | AnchorHigh, | ||
| double | LowpassFilter[], | ||
| double | HighpassFilter[], | ||
| cvbdim_t | LengthFilter, | ||
| IMG & | ImgApproximation, | ||
| IMG & | ImgDetailX, | ||
| IMG & | ImgDetailY, | ||
| IMG & | ImgDetailXY | ||
| ) |
This function performs the two-dimensional wavelet decomposition on the input image.
Multi-resolution transformation has been recognised as a very useful approach to analyse the information content of images. The wavelet transform is a signal analysis tool that provides a multi-resolution decomposition of an image using (bi-)orthogonal base functions and results in a non-redundant image representation. The base functions are called wavelets, and they are generated from one single function, called mother wavelet, by dilations and translations.
In a two-dimensional transform, the wavelets measure intensity variations along different directions (along columns and rows) highlighting details in three different orientations (horizontal, vertical, and diagonal).
The forward/inverse wavelet transform use the fast polyphase algorithm which is equivalent to traditional application of separable convolution and dyadic resampling in different order. The following image shows the discrete wavelet decomposition:
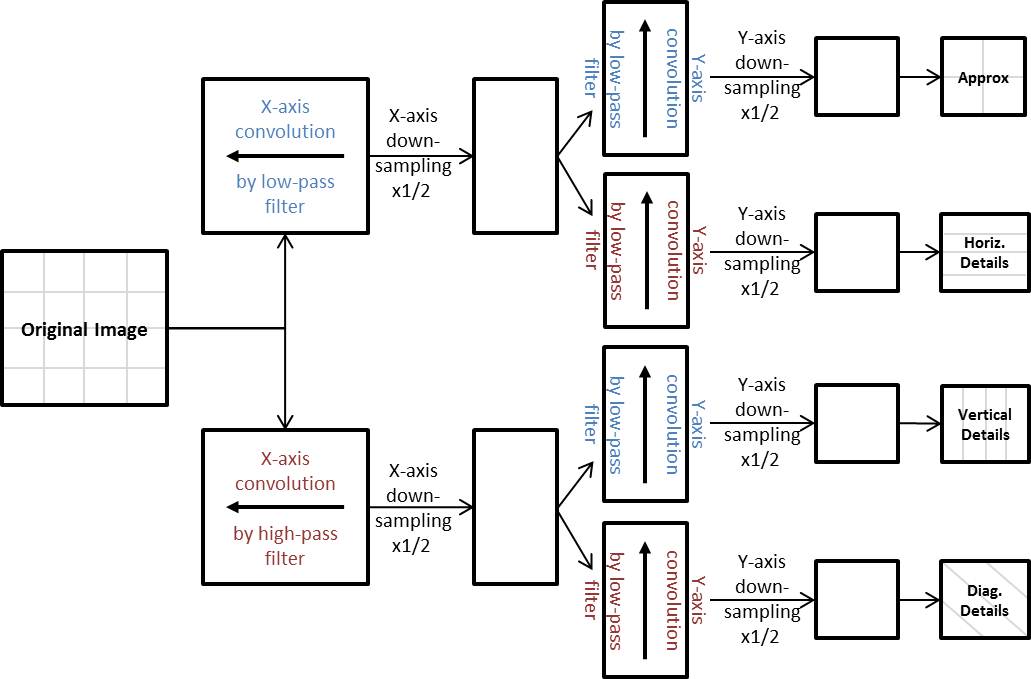 Image: Intel Integrated Performance Primitives, Reference Manual, Volume 2: Image and Video Processing. Ipp 7.0
Image: Intel Integrated Performance Primitives, Reference Manual, Volume 2: Image and Video Processing. Ipp 7.0
The decomposition components have following meaning:
The filter bank consists of two analysis filters and includes the low-pass decomposition filter (or coarse filter) and the high-pass decomposition filter (or detail filter). The parameters AnchorLow and AnchorHigh describe the filter offset within the low-pass/high-pass filter. The anchor value sets the initial leftmost filter position
relative to image row or column as shown in the following image (where N is LengthFilter):
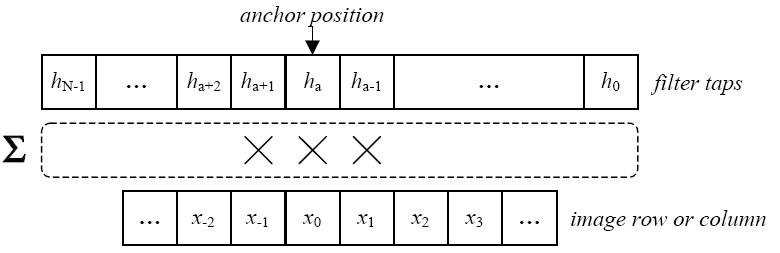 Image: Intel Integrated Performance Primitives, Reference Manual, Volume 2: Image and Video Processing. Ipp 7.0
Image: Intel Integrated Performance Primitives, Reference Manual, Volume 2: Image and Video Processing. Ipp 7.0
If you use the pre-defined filters (see TWaveletFilter for more information) you can pass 0 to the properties LowpassFilter, HighpassFilter, and LengthFilter.
| [in] | ImgIn | Handle of source image to compute wavelet decomposition for. |
| [in] | FilterType | Wavelet/Scaling filters to be applied in the filter bank. Choose either pre-defined filters or apply a custom defined filter. See TWaveletFilter for more information. |
| [in] | AnchorLow | Anchor position within low-pass (scaling) filter. This value must be between 0 and LengthFilter - 1. |
| [in] | AnchorHigh | Anchor position within high-pass (wavelet) filter. This value must be between 0 and LengthFilter - 1. |
| [in] | LowpassFilter | Filter coefficients of low-pass filter. This parameter is only used when WT_CUSTOM is used as filter type (FilterType). |
| [in] | HighpassFilter | Filter coefficients of high-pass filter. This parameter is only used when WT_CUSTOM is used as filter type (FilterType). |
| [in] | LengthFilter | Length of high-pass and low-pass filter. |
| [out] | ImgApproximation | Handle off low-pass sub-image (approximation). |
| [out] | ImgDetailX | Handle of detail image representing vertical variations. |
| [out] | ImgDetailY | Handle of detail image representing horizontal variations. |
| [out] | ImgDetailXY | Handle of detail image representing diagonal variations. |
| cvbres_t InverseWaveletTransform | ( | TWaveletFilter | FilterType, |
| cvbdim_t | AnchorLow, | ||
| cvbdim_t | AnchorHigh, | ||
| double | LowpassFilter[], | ||
| double | HighpassFilter[], | ||
| cvbdim_t | LengthFilter, | ||
| IMG | ImgApproximation, | ||
| IMG | ImgDetailX, | ||
| IMG | ImgDetailY, | ||
| IMG | ImgDetailXY, | ||
| IMG & | ImgOut | ||
| ) |
This function performs the two-dimensional inverse wavelet transform on the sub-images.
The following image shows the discrete wavelet reconstruction:
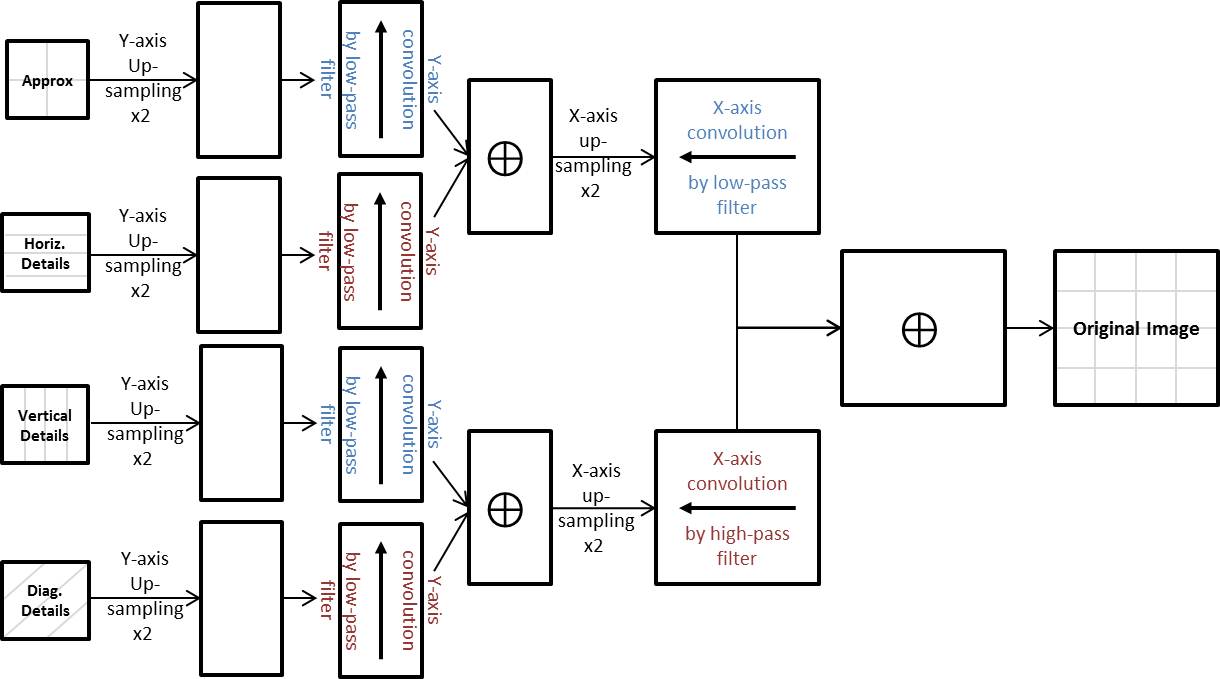 Image: Intel Integrated Performance Primitives, Reference Manual, Volume 2: Image and Video Processing. Ipp 7.0
Image: Intel Integrated Performance Primitives, Reference Manual, Volume 2: Image and Video Processing. Ipp 7.0
The filter bank consists of two synthesis filters and includes the low-pass reconstruction filter (or coarse filter) and the high-pass reconstruction filter (or detail filter). The parameters AnchorLow and AnchorHigh describe the filter offset within the low-pass/high-pass filter. The anchor value sets the initial leftmost filter position relative to image row or column as shown in the following image (where N is LengthFilter):
 Image: Intel Integrated Performance Primitives, Reference Manual, Volume 2: Image and Video Processing. Ipp 7.0
Image: Intel Integrated Performance Primitives, Reference Manual, Volume 2: Image and Video Processing. Ipp 7.0
1. | [in] | FilterType | Wavelet/Scaling filters to be applied in the filter bank. Choose either pre-defined filters or apply a custom defined filter. See TWaveletFilter for more information. |
| [in] | AnchorLow | Anchor position within low-pass (scaling) filter. This value must be between 0 and LengthFilter - 1. |
| [in] | AnchorHigh | Anchor position within high-pass (wavelet) filter. This value must be between 0 and LengthFilter - 1. |
| [in] | LowpassFilter | Filter coefficients of low-pass filter. This parameter is only used when WT_CUSTOM is used as filter type (FilterType). |
| [in] | HighpassFilter | Filter coefficients of high-pass filter. This parameter is only used when WT_CUSTOM is used as filter type (FilterType). |
| [in] | LengthFilter | Length of high-pass and low-pass filter. |
| [in] | ImgApproximation | Handle off low-pass sub-image (approximation). |
| [in] | ImgDetailX | Handle of detail image representing vertical variations. |
| [in] | ImgDetailY | Handle of detail image representing horizontal variations. |
| [in] | ImgDetailXY | Handle of detail image representing diagonal variations. |
| [out] | ImgOut | Handle of result image to store reconstructed image in. |